How To Build A Quantum Tic-Tac-Toe Game Using Python And Qiskit.
A simple game to introduce you to Quantum programming using the Qiskit SDK

A simple game to introduce you to Quantum programming using the Qiskit SDK
Tic-Tac-Toe.
Also known as Xs and Os, tic-tac-toe is a two-player game whereby the players take turns marking spaces in a three-by-three grid with 'X' or 'O'. Any player who succeeds in placing their markings in a row(vertical, horizontal, or diagonal) wins the game. Players can also draw/tie if they both fail to make their markings in a row.
Quantum Computing.
I read somewhere that, "Anything seems fancy if you add the word Quantum to it". This statement couldn't be truer. While there are very technical terms with the word Quantum(e.g Quantum cryptography, Quantum Computing, Quantum Time Travel), there can also be nonsensical words with the word Quantum(e.g Quantum Alfaxad, Quantum recipes, Quantum pencil), see how fancy these words appear?
The Quantum computing field has become popular in recent years, the hype lies around the potential that quantum computing has to solve various problems even better than classical computers, problems such as weather forecasting, drug designing, and financial markets analysis. Quantum computing is made possible with mainly two properties: Superposition and Entanglement.
Superposition & Entanglement.

Just as in classical computers we have bits('1' or '0'), in quantum computers we have qubits(quantum bits). Qubits are represented by states |0> or |1>. The ability of qubits to be in multiple states is what is known as superposition.
However, in entanglement, two members of a pair (e.g |0> and |1> states) can exist in a single quantum state. Changing the state of one of the qubits will instantaneously change the state of the other one in a predictable way. This happens even if they are separated by very long distances. In simple terms, the difference between superposition and entanglement is as follows: an entangled state is a superposed state but not all superposed states are entangled.
Quantum Tic-Tac-Toe.
Now let's get to the most interesting part. We will use the above principles to create a tic-tac-toe game. We will focus on the underlying principles and rules of the game instead of high-level game development. We are going to use Python and the Qiskit SDK. Qiskit is an open-source SDK by IBM for working with quantum computers and simulators at the level of pulses, circuits, and application modules.
Game Rules.
- The game has 9 tiles, each corresponds to a real qubit!
- The game has 2 players, player 1 and player 2.
- They take turns as in classical tic tac toe marking one tile at a time.
- Player 1 marks a tile with a |0> and player 2 makes a tile with a |1>.
This quantum tic tac toe has a twist. During a player turn, a player can decide to entangle two tiles instead of marking a tile. If that is the case, then the entangled tiles can not be marked for any other player during the game.
Once all the tiles are marked or entangled the quantum circuit of the game is initialized and the qubits are measured revealing the final state of the game. An error-correcting algorithm makes sure that there was no errors. If there are errors the code is run again until there are no errors. Whoever has 3 in a line wins. If both will then the code is run again until one wins.
Code.
I assume you have prepared your python virtual environment. The only thing you need to install is Qiskit.
$ pip install qiskitLet's get started !!!
First, we import necessary libraries from Qiskit SDK.
#import necessary modules
from qiskit import QuantumCircuit, QuantumRegister, ClassicalRegister
from qiskit import execute, assemble, BasicAer
from qiskit.visualization import plot_histogram
from qiskit.tools.monitor import job_monitorTic-tac-toe layout
### tic toc toe ###
######################################
# # # #
# 6 # 7 # 8 #
# # # #
######################################
# # # #
# 3 # 4 # 5 #
# # # #
######################################
# # # #
# 0 # 1 # 2 #
# # # #
######################################
Now, give an overview of the gameplay. We will explicitly define board states for players 1 and 2
#By default player1 tiles are initilized to \0> state
# Player2 tiles initialized |1> state
######
#This variables can be inputed by the users to change the input of the game!
l_player_1 = [0] #list of qbits cell numbers inicialized to 0(player1 tiles)
l_player_2 = [2,3] #list of qbits cell numbers inicialized to 1(player 2 tiles)
l_entangled = [(1,6),(7,8),(4,5)] #list of pairs of cells that need to be entangled to |01>+|10>Then we convert the given lists into a quantum state matrix.
#translate from lists to initial state matrix
l_initial_ordered = [0,0,0,0,0,0,0,0,0]
for inx in range(len(l_player_1)):
l_initial_ordered[l_player_1[inx]]=0
for inx in range(len(l_player_2)):
l_initial_ordered[l_player_2[inx]]=1
entg_num = 1
for inx in range(len(l_entangled)):
l_initial_ordered[l_entangled[inx][0]]='e'+str(entg_num )
l_initial_ordered[l_entangled[inx][1]]='e'+str(entg_num )
entg_num +=1
print('This the initial table state inputed by the user:\n0 corresponds to player 1, 1 corresponds to player 2,\n e1,e2,e3... corresponds to entangled tiles')
print('-----\n'+str(l_initial_ordered[6])+'|'+str(l_initial_ordered[7])+'|'+str(l_initial_ordered[8]))
print('-----\n'+str(l_initial_ordered[3])+'|'+str(l_initial_ordered[4])+'|'+str(l_initial_ordered[5]))
print('-----\n'+str(l_initial_ordered[0])+'|'+str(l_initial_ordered[1])+'|'+str(l_initial_ordered[2]))
print('-----')[Output]
This the initial table state inputed by the user:
0 corresponds to player 1, 1 corresponds to player 2,
e1,e2,e3... corresponds to entangled tiles
--------
e1|e2|e2
--------
1|e3|e3
--------
0|e1|1
--------We then define a 9-qubit Quantum to represent the tiles.
#Quantum circuit to represent the tiles
# Create a Quantum Circuit acting on the q register
circuit = QuantumCircuit(9, 9)
circuit.name = "Tic toc toe"
for inx in range(len(l_player_2)):
circuit.x(l_player_2[inx])
for inx in range(len(l_entangled)):
circuit.h(l_entangled[inx][0]) #hardamard gate
circuit.x(l_entangled[inx][1]) #x gate
circuit.cx(l_entangled[inx][0],l_entangled[inx][1]) #controlled-x gate
circuit.measure(list(range(9)), list(range(9)))
# Print out the circuit
print('This is the corresponding quantum circuit from the users input')
#draw circuit
circuit.draw(output='mpl', filename='circuit.png')[Output]
This is the corresponding quantum circuit from the users input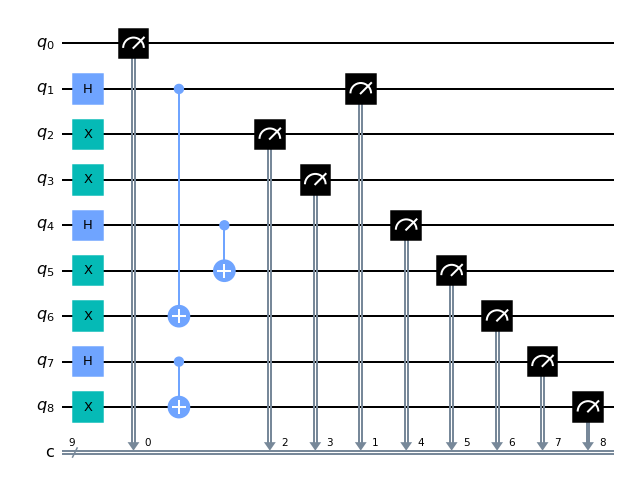
We then write the rules to define a game winner. Once the entangled tiles collapse, one tile is randomly selected to decide a game winner.
# Check winner
def check_winner(board,mark):
return(((board[0]==mark) and (board[1]== mark) and (board[2]==mark) )or #for row1
((board[3]==mark) and (board[4]==mark) and (board[5]==mark) )or #for row2
((board[6]==mark) and (board[7]==mark) and (board[8]==mark) )or #for row3
((board[0]==mark) and (board[3]==mark) and (board[6]== mark) )or#for Colm1
((board[1]==mark) and (board[4]==mark) and (board[7]==mark) )or #for Colm 2
((board[2]==mark) and (board[5]==mark) and (board[8]==mark) )or #for colm 3
((board[0]==mark) and (board[4]==mark) and (board[8]==mark) )or #diagonal 1
((board[2]==mark) and (board[4]==mark) and (board[6]==mark) )) #diagonal 2
flag_p1=1
flag_p2=0
while (flag_p1 or flag_p2) and not(flag_p1 and flag_p2):
print('Running the quantum circuit...')
flag_p1=0
flag_p2=0
job = execute(circuit, BasicAer.get_backend('qasm_simulator'), shots=1)
result = job.result()
l_final_ordered=list(map(lambda x: int(x),list(list(result.get_counts().keys())[0][::-1])))
print(l_final_ordered)
#list with ordered cells
print('The colapsed state is:')
print('-----\n'+str(l_final_ordered[6])+'|'+str(l_final_ordered[7])+'|'+str(l_final_ordered[8]))
print('-----\n'+str(l_final_ordered[3])+'|'+str(l_final_ordered[4])+'|'+str(l_final_ordered[5]))
print('-----\n'+str(l_final_ordered[0])+'|'+str(l_final_ordered[1])+'|'+str(l_final_ordered[2]))
print('-----')
if (check_winner(l_final_ordered,0) ):## to check if player 1 won
print('Player 1 won!')
flag_p1 = 1
else:
flag_p1 = 0
if (check_winner(l_final_ordered,1)): ## to check if player 2 won
print('Player 2 won!')
flag_p2 = 1
else:
flag_p2 = 0
if (flag_p1 or flag_p2) and not(flag_p1 and flag_p2):
break
if flag_p1 and flag_p2:
print('The game will repeat until one one player wins')
if not(flag_p1 and flag_p2):
print('No winners,\nThe game will repeat until one one player wins')
Once the above snippet runs, you will get an output from the quantum circuit which will then be represented on the tic-tac-toe. Also, results in this tutorial may differ to yours since they depend on random selection of collapsed states of entangled tiles.
[Output]
Running the quantum circuit...
[0, 0, 1, 1, 0, 1, 1, 1, 0]
The colapsed state is:
-----
1|1|0
-----
1|0|1
-----
0|0|1
-----
Player 1 won!Hooray!!! you just built your first quantum circuit and got familiar with some quantum computing concepts and tic-tac-toe :)
What's Next?
Now that you got familiar with the concepts, subscribe to bi-weekly articles to assist you in your quantum computing/development journey. We will explore basic concepts from quantum states and circuits to building games and other advanced concepts like optimization and Quantum Machine Learning(QML). Feel free to also check further readings below.
Further Readings.
- https://qiskit.org/
- https://qiskit.org/textbook-beta/course/introduction-course
- https://learn.qiskit.org/course/introduction/why-quantum-computing
- https://eandt.theiet.org/content/articles/2019/04/quantum-for-dummies-the-basics-explained/#:~:text=Superposition is a system that,spin up and spin down.&text=Only when it is measured,one position or the other.
- https://www.technologyreview.com/2019/01/29/66141/what-is-quantum-computing/#:~:text=Qubits have some quirky quantum,and another is called entanglement.